Nonlinear Exceptional Points with a Complete Basis 

                            in Dynamics

 Professor Xiao Meng's team from Wuhan University, in collaboration with Associate Professor Wan Duanduan's team, has pioneered research on the effects of nonlinear gain on non-Hermitian exceptional points. They have proposed and experimentally verified the existence of exceptional points with a complete basis in the dynamical process. The related research results were published under the titles "Nonlinear Exceptional Points with a Complete Basis in Dynamics" and "Observation of Exceptional Nonlinear Points with a Complete Basis in Dynamics" in the journal Physical Review Letters. The corresponding authors of the paper are Professor Xiao Meng and Associate Professor Wan Duanduan, with the first author being Bai Kai, a doctoral student at Wuhan University. Additionally, Wuhan University doctoral student Fang Liang, Liu Tian-rui, master's student Li Jia-zheng, and undergraduate student Lin Chen also made outstanding contributions to this subject.

An exceptional point (EP) is a type of special spectral singularity where two or more eigenmodes coalesce, causing their eigenvectors to become identical, and as a result, the completeness of the Hamiltonian's eigenbasis is lost. The unique physical properties near EPs have led to various novel applications, such as signal amplification, laser mode resolution, detection of minute signals, quantum sensing, energy transfer, photonic chips, unidirectional lasers, quantum control, mode conversion, and more. However, as the parameters approach an EP, the system noise significantly increases due to the eigenvectors becoming identical, which can greatly hinder the realization of the aforementioned applications. To address this, we introduce the concept of a nonlinear exceptional point (NEP). While maintaining the fundamental characteristics of a linear EP, it restores the completeness of the effective Hamiltonian's eigenbasis in the dynamical process, fundamentally solving the noise divergence issue caused by the aggregation of eigenbasis vectors. 

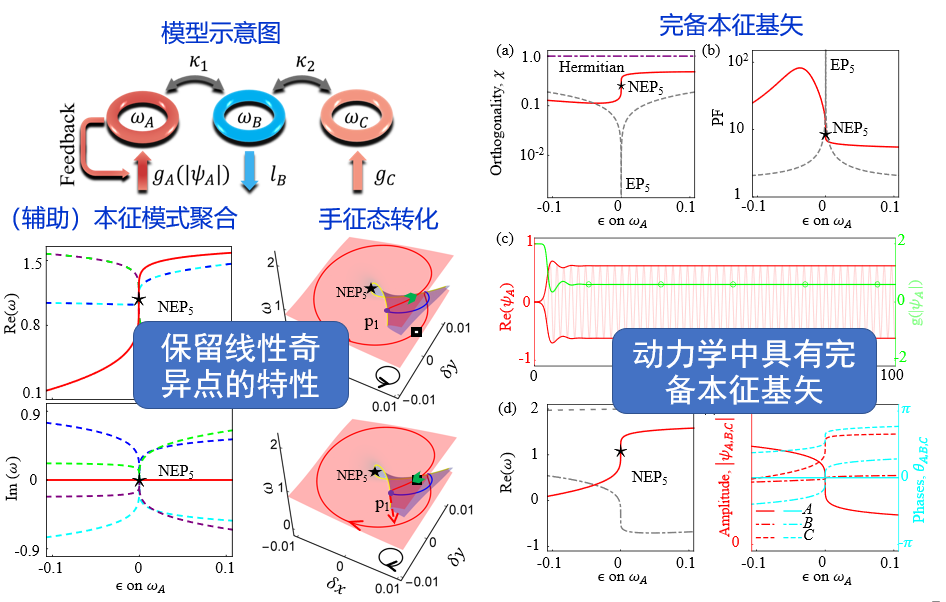
Left panel shows the key features of EPs, the right panel shows the complete basis in dynamics.

Subsequently, we designed the minimal model for observing NEP, and observed a NEP₃ based on circuit experiments.

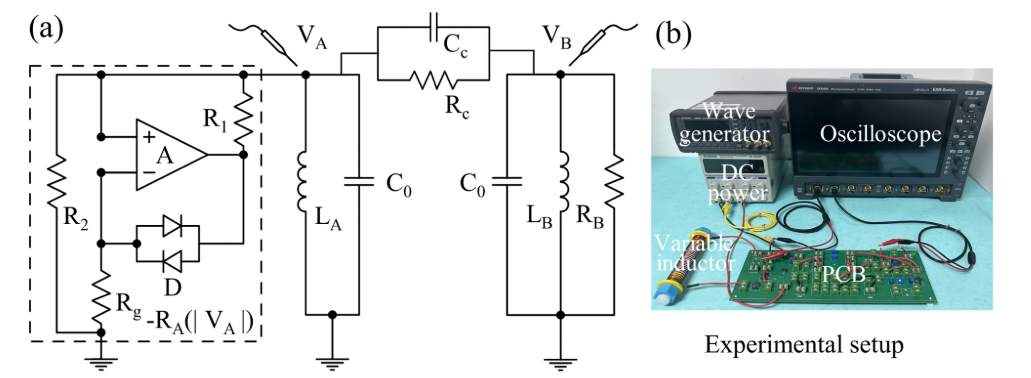
(a) The circuit used in the experiment (b) A photo of the experimental setup.

Link：https://link.aps.org/doi/10.1103/PhysRevLett.132.073802

Link：https://link.aps.org/doi/10.1103/PhysRevLett.130.266901