显著增强信噪比的非线性奇异联结点

  武汉大学物理学院肖孟教授与万端端特聘副研究员合作，开拓非线性饱和增益对非厄米奇异点的研究，并提出了具有显著增强信噪比（SNR）的非线性奇异联结点（EX）, 相关研究成果以” Nonlinearity enabled higher-order exceptional singularities with ultra-enhanced signal-to-noise ratio” 为题发表在National Science Review期刊上。该论文的通讯作者为武汉大学肖孟教授和万端端特聘副研究员，第一作者为武汉大学博士研究生白凯。此外，武汉大学博士研究生方亮、刘天瑞和武汉大学硕士研究生李佳铮也为该课题做出了突出贡献。

  在数学和物理的基础研究中，奇点及其邻域的特性总是能引起研究者广泛兴趣。在非厄米系统中，EP点作为一类特殊的奇点，得益于一系列与EP点相关的新奇物理现象和潜在的应用被阐述，如信号放大、拓扑能量转移、微小信号探测等而备受关注。然而，真实的EP点（特别是高阶EP）在实现过程中受到严格的参数要求和不可避免的噪音破坏的影响。在微小信号探测领域，EP点是否能提高传感器的SNR引发了持续的争论。

  本项工作，开拓研究非线性饱和增益对奇异点的形成，新物理和应用方面的贡献。理论和电路实验验证，形成EX点所需的参数数目从线性系统中的6个参数降低到了2个。同时，得益于非线性饱和增益的反馈机制，系统在动力学演化过程中，达到并保存在一个稳态附近，一些基础的分辨率限制和因为本征模式非正交而增强的系统噪音被抑制。 因而可以同时显著增强响应率和SNR，可以极大的改善传感器的性能，进一步促进非线性和非厄米领域的交叉。

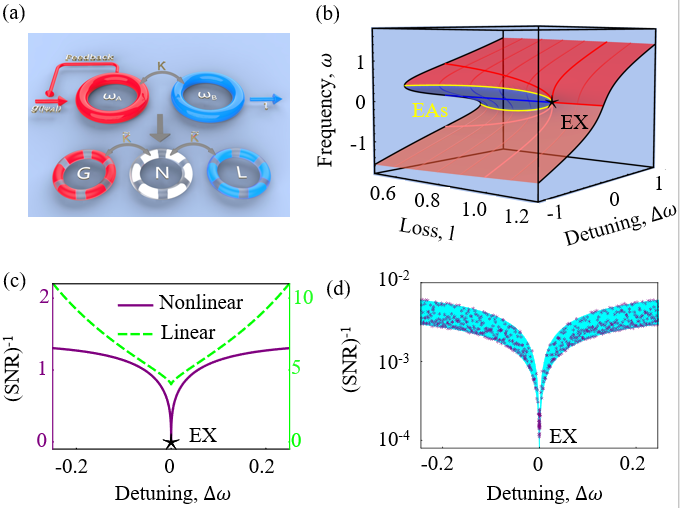
(a),上半部分展示了非线性双腔耦合系统，下半部分为线性三腔耦合系统。（b）非线性薛定谔方程的定态解（红色和蓝色区域表示稳定的定态解和非稳定的定态解）。(c), 从稳定的定态解出发计算(SNR)-1。(d) 系统动力学演化过程中提取(SNR)-1。

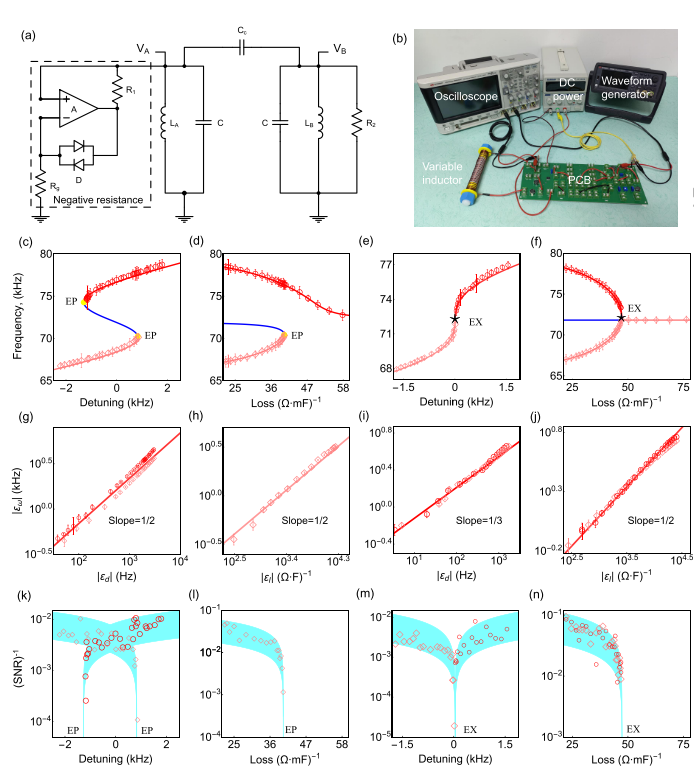
（a）电路实验示意图。 （b）一张真实的电路实验的照片。（c-f）实验测量频率随着系统参数的变化曲线。（g-j）对数坐标系下的斜率反应其对应的奇异点的邻域行为。（k-n）在相应奇异点处，展现出巨大的信噪比（SNR）的增强。

全文链接：https://doi.org/10.1093/nsr/nwac259